50 ACT Math Formulas You Need to Know
Numbers and Quantities


1. Arithmetic Sequences
an = a1 + (n − 1)d
This formula defines a sequence of numbers where the difference between each consecutive term is the same. The first term of the sequence is a1, the nth term of the sequence is an, and the constant difference between consecutive terms is d.
2. Geometric Sequences
This formula defines a sequence of numbers where given the first term, each successive term is defined by multiplying the previous term by a fixed number, also known as the common ratio (r). As with arithmetic sequences, the first term of the sequence is a1, and the nth term of the sequence is an.

3. Logarithms

logb(bx) = x
Logarithms are the inverse functions of exponents. In other words, the logarithm of a number, x, is the exponent to which another number, the logarithmic base b, must be raised to produce x. You’ll likely need to rewrite logarithms on the ACT using the following formulas:
If logb(x) = y, then by=x.
logb(xy) = logb(x) + logb(y)
logb(xy) = logb(x) − logb(y)

d = r t
This is a common algebraic relationship where d is distance, r is rate, and t is time. You can rewrite this equation to isolate r or t, and “distance” can be replaced with the more general concept of “quantity.” Just be sure to keep your units straight!
5. Function Notation
f∘g(x)=f(g(x))
This is a composite function, where the output of g(x) is the input for f(x).
Notice that f∘g(x) is different from fg(x)=f(x)×g(x).
6. Radians to Degrees
π radians = 180∘
This is a useful conversion to memorize for trigonometry problems, especially those involving the coordinate plane. To boost your speed, make sure to have the unit circle memorized!
Graphs and Coordinate Geometry

7. Slope of a Line
(y2 − y1)/(x2 − x1) = m
Slope is a rate, specifically rise/run. The slope of any line, m, can be determined given any two points on the line, (x1, y1) and (x2, y2).
8. Slope-Intercept Formula
y = mx + b
This equation defines a line with slope m and a y-intercept of (b, 0) that passes through the point (x, y).
9. Distance Formula
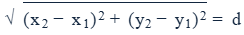
This formula calculates the distance, d, between two points (x1, y1) and (x2, y2).
10. Midpoint Formula
((x1 + x2)/2, (y1 + y2)/2)
This formula defines the midpoint of the line between two points, (x1, y1) and (x2, y2).

11. FOIL (First, Outer, Inner, Last)
(a + b)(c + d) = ac + ad + bc + bd
We use FOIL to multiply 2 binomials together. Below are some FOIL shortcuts to memorize, where y is a constant:
(x + y)(x + y) = (x + y)2 = x2 + 2xy + y2
(x − y)(x − y) = (x − y)2 = x2 − 2xy + y2
(x + y)(x − y) = x2 − y2
12. Quadratic Formula
If ax2 + bx + c = 0, then x =
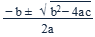
The quadratic formula provides values of x, also known as solutions/roots/zeros, for a given quadratic function ax2+bx+c=0, where a, b, and c are constants. The expression underneath the square root, b2−4ac, is called the discriminant and determines the number of solutions. Specifically:
- If b2 − 4ac < 0, then there are 2 real solutions (i.e. values of x)
- If b2 − 4ac = 0, then there is 1 real solution
- If b2 − 4ac > 0, then there are no real solutions
13. Vertex Form
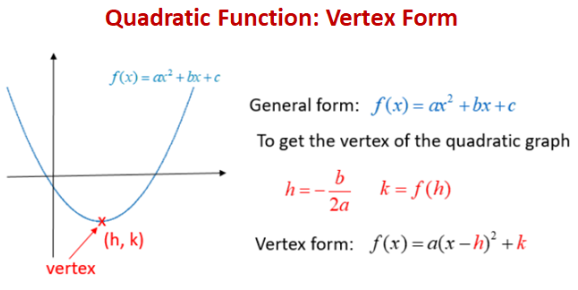
y = a(x − h)2 + k
This formula defines a quadratic function with the vertex at (h,k) and a constant, a, determining stretch and direction. The axis of symmetry is line x=h, which crosses the vertex.
Note that FOIL will convert this equation to an expanded form. As such, you may be asked to factor back into vertex form in order to provide coordinates for the vertex.

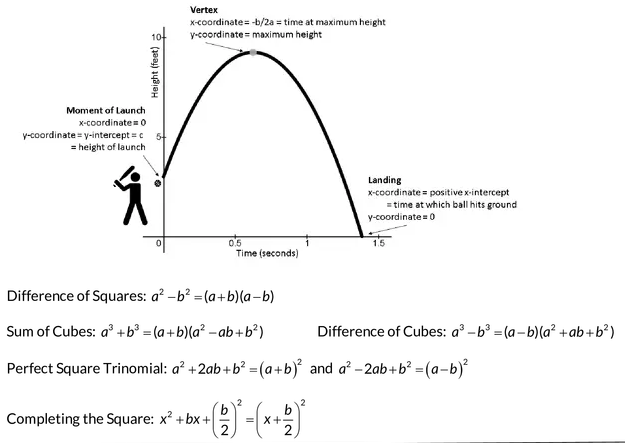
14. Graphing Circles
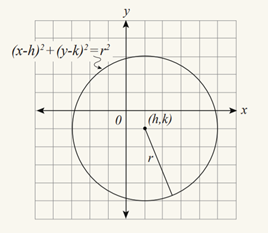
(x − h)2 + (y − k)2 = r2
This equation defines a circle with center point (h, k) and radius r. As with the quadratic function above, FOIL will convert this equation to an expanded form, and you may be asked to factor in order to find the radius or central coordinates.
Plane Geometry
15. Angles and Lines
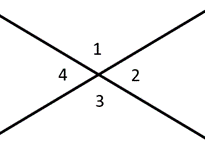
Angles along a line are called supplementary angles, adding up to 180∘. Complementary angles add up to 90∘, a right angle. Vertical angles describe angles directly across from one another, which are always congruent. In the diagram to the left, for example, we would say that angles 1 & 2 are supplementary, while angles 1 & 3 are vertical angles.

16. Area of a Triangle
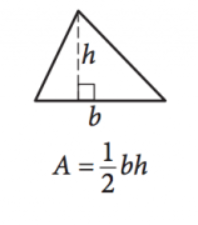
1/2 b h = A
This equation provides the area (A) of any triangle given lengths of the base (b) and height (h). Note that height is the length of the line extending at a complementary angle from any side (the base) up to the point/angle directly across from that side.
For equilateral triangles, where all three sides (s) are the same length, the area equation is:
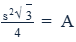
17. Pythagorean Theorem
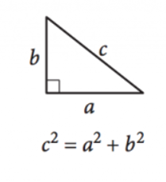
As angles in a triangle always add up to 180∘, a right triangle is defined as any triangle with one right angle, ensuring the other two angles are complementary. The side lengths of right triangles can be defined by the Pythagorean Theorem:
a2 + b2 = c2
Here, a and b are the lengths of the legs, or the sides across from the complementary angles, and c is the length of the hypotenuse, the side across from the right angle.
It may be helpful to also memorize the following Pythagorean triples, or values for side lengths (a,b,c): 3 – 4 – 5, 5 – 12 – 13, 7 – 24 – 25, and 8 – 15 – 17. Note that the hypotenuse is always the longest side.
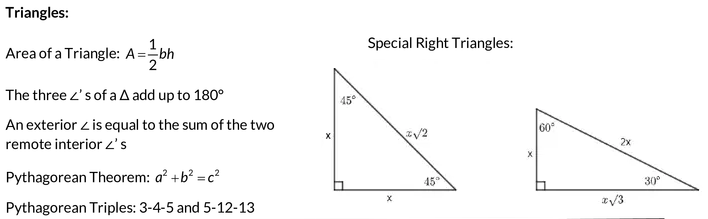
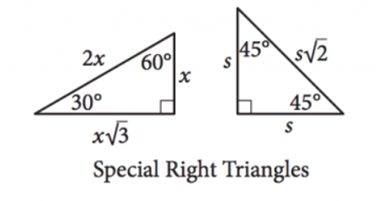
18. Special Right Triangles
There are two types of special right triangles, which have the angles and length ratios as follows:

19. Areas of Quadrilaterals
A = lw
This formula provides the area of a rectangle with length l and width w.
A = bh
This formula provides the area of a parallelogram given base b , the length of the longest sides, and height h, defined as the length of the line extending at a complementary angle up from one base to the other.
A = (b1 + b2) / 2 × h
This formula provides the area of a trapezoid with bases b1 and b2 and height h, defined the same way as for parallelograms.
20. Interior Angles of Regular Polygons
(n − 2) × 180∘ = S
In a regular polygon, where all sides and angles are equal, this formula provides the sum (S) of the interior angles given a polygon with n sides and angles. We can also find each interior angle by calculating Sn.
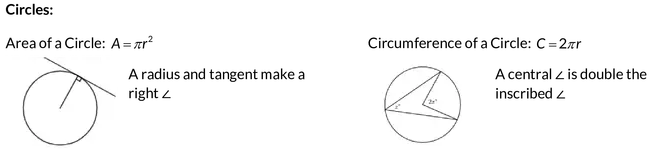

21. Arc Length in a Circle
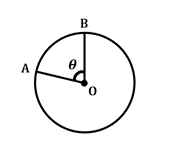
θ / 360∘ × 2πr = arc length
This formula defines the length of the arc, or section of the circle circumference, between two given radii intersecting at the circle center with central angle θ. Note that the 2πr incorporates circle circumference into this formula.
22. Sector Area in a Circle
θ / 360∘ × πr2 = sector area
Similar to arc length, this formula provides the area of the sector between two given radii intersecting at the circle center with central angle . The πr2 incorporates circle area into this formula.
23. 3D Shapes
SA = 2(lw + wh + lh)
V = lwh
These formulas provide the surface area (SA) and volume (V) for a rectangular prism with length l, width w, and height h.
V = πr2h
This is the volume formula for a right cylinder with base radius r and height h.
Should you need the surface area or volume formulas for any other 3D shapes, the ACT will provide relevant formulas in the questions themselves.
Trigonometry
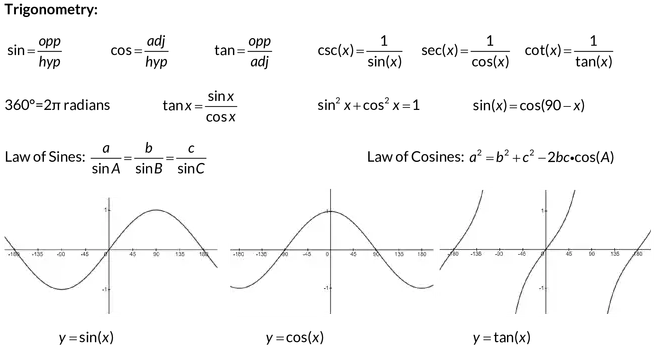

24. SOH-CAH-TOA
Most ACT trig problems involve manipulating sine, cosine, and tangent, which are calculated as follows for given angle x in a right triangle:
sin(x) = opposite leg / hypotenuse
cos(x) = adjacent leg / hypotenuse
tan(x) = opposite leg / adjacent leg = sin(x) / cos(x)
SOH-CAH-TOA is an easy mnemonic for remembering which trig function corresponds to which side lengths!
25. Cofunction Identities
sin(x) = cos(90∘ − x)
cos(x) = sin(90∘ − x)
In words, these identities show that a trig function of angle x equals the value of the cofunction of the complement of x. They are generally used when dealing with more advanced trigonometry, allowing for easy conversions between sine and cosine.
26. Ratio/Reciprocal Trig Identities
You may occasionally see the reciprocal identities of sin(x), cos(x), and tan(x), which are:
csc(x) = 1 / sin(x)
sec(x) = 1 / cos(x)
cot(x) = 1 / tan(x)
27. Pythagorean Identity
sin2(x) + cos2(x) = 1
Based on the Pythagorean Theorem and the unit circle, this identity is generally used alongside the cofunction identities to solve trig problems (sans calculator) where angle x or the values of these trig functions of x are unknown.
Statistics and Probability

28. Percentages
n% of m = n/100 × m
Percentages are used to express parts of a whole, and the % symbol generally means “divide by 100.” As such, the above equation answers any problem asking for n% of quantity m.
29. Mean, Median, Mode, and Range
The ACT tests basic statistical knowledge, generally involving the measures below:
- Mean is the average, or sum of all terms / total number of terms
- Median is the middle term, or the average of the two middle terms if there is an even number of terms
- Mode is the term(s) that occurs most frequently
- Range is the difference between the largest and smallest terms
30. Probability
P(A) = number of desired outcomes / total number of possible outcomes
Probability represents the likelihood of an event (A) occurring, calculated by dividing the number of desired outcomes by the number of total possible outcomes. For instance, the probability of rolling a 6 on an even-sided dice is 16.
31. Independent Events
P(A and B) = P(A) × P(B)
Events A and B are independent if A occurring does not affect the probability of B occurring. To calculate the probability that both independent events will occur, we multiply their individual probabilities together. For instance, the probability of flipping heads twice is 1/2 × 1/2 = 1/4.
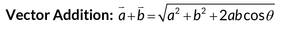
Matrices
Finally, every few tests there’s a question about matrices. Students who are chasing a high score on the ACT should make sure that they know how to add and multiple matrices:
Given two matrices A and B



Leave a Reply