Special Right Triangles

There are certain special triangles that students might be expected to know on the math section of the ACT. Like the formulas for the area of a circle or rectangle, these identities are normally presented to students at the beginning of the test, and so the challenge is knowing how to identify problems where these identities are relevant and how to use them to solve relevant problems.

The most common special triangles are: 45-45-90 and 30-60-90 triangles.

Because these length and angle relationships are set, any time these angles appear or these side lengths appear, they can give us useful information for solving a problem. Problems involving these triangles often utilize words/drawings or the xy-plane. They are also often relevant on problems involving triangles and points of tangency. For example:

Since the square touches both the center and the perimeter of the triangle, a line going from one corner of the square to the other corner will be equal to the radius of the circle. This straight line divides the square perfectly in half, which means that the angles on each side of the line are = 45 degrees. That means that this square can be defined as follows:

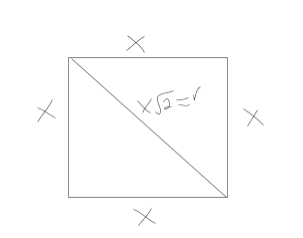
The question gives us the area of the shaded region, which equals 36π − 18. From the image, it’s clear that this is equal to the area of the circle minus the area of the square. In other words:

πr² − s² = 36π − 18 where r is the radius of the circle and s is the side lengths of the square. The triangle above shows that r = x. Plugging this into the formula above gives:

π(x)² − x²  = 36π − 18

2x²π − x² = 36π − 18

x²(2π−1)  = 18(2π−1)

x² = 18 x= x = 3

x was equal to the side length of the square and the question asks for the perimeter of the square. Therefore, the answer is: 4(3) = 12 and so C is the correct answer.