Radicals

Radicals (also known as “roots”) are the opposite of exponents. The most common radical that students are familiar with is the square root or root-2, which is why the default radical symbol is also the square root symbol: . A square root basically says: to get the number under the square root, what number would need to be multiplied by itself to get that number?

Roots above a square root will have a subscript next to the root to show what “degree” the root is taken to. Again, this is the same as exponents where X³ means x cubed. In the same way, 

x−−√3 is the cube root of x. The first expression says what happens when x is multiplied by itself 3 times. The second expression asks what would need to be multiplied by itself three times to get x.

Radical Operations

Cancel Out

Because radicals and exponents express opposite operations, they can cancel out with each other under certain circumstances. For example, a square root and an exponent of 2 will cancel out with each other.

 = x The same thing is true for any evenly balanced roots and exponents

x3−−√3=x

Multiplication

Two separate square roots multiplied by each other are equivalent to the square root of the products of those numbers

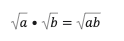
Simplification

The rule above can also be used to help simplify square roots. Instead of combining square roots though, it will involve separating them.

For example, take the square root of 48. This is equal to the product of the roots of its factors: sqrt(48) = sqrt(4⋅12). The square root of 12 is not a whole number, but the square root of 4 is.

Therefore, the expression can be simplified as 2sqrt(12). There are still only whole numbers here, but now if there was a or a 2 in the denominator below , it would be clear that these would cancel out and that the expression could be simplified further.

Whenever a root appears with a whole number underneath it, students should ask themselves: “is there a way to factor this number such that I can simplify the expression?”

This also works when there are variables under the root.  

Division

Division with roots is the opposite of multiplication. The ratio of the square roots of two numbers is equal to the square root of the ratio of those two numbers.

Fractional Exponents

As mentioned in the exponents section, roots can be expressed as fractional exponents. If a number has a fractional exponent, then the denominator (bottom half) of that fractional exponent is the root that that number is being taken to.

x12= This doesn’t affect or change exponents in the denominator. Those remain in the normal exponent spot, even when the fractional exponent is converted to the root form:

x32=