Probability

The probability of an event occurring is equal to the number of successful outcomes (outcomes that fulfill the pre-set criteria) divided by the number of potential outcomes.

For example, to calculate the probability of drawing a red skittle from a bag of skittles, a student will need two pieces of information:

1. How many red skittles are there in one bag
2. How many total skittles (regardless of color) are there in one bag

The probability of drawing a red skittles is then equal to: # of red skittles / # of total skittles.

The key for probability questions is whether the question is asking us to add or multiply probabilities together.

• Adding Probabilities: Add probabilities when there are multiple different possibilities that will fulfill the probability criteria. So add each discrete probability together to get the total probability.

How does a student know if there are multiple different possibilities that will fulfill the criteria? In the problem above, it is not specified that a particular red skittle is needed (e.g. the heaviest or the largest). Any red skittle will do, so the total probability adds together the individual probability of getting each individual red skittle and that gives the probability of getting a red skittle.

The main key word for an added probability question is: OR. If scenario A or B could be a success, then the probability of being successful is = the probability of A + the probability of B (as long as these two things are not mutually exclusive. In other words, that there is no overlap between these possible outcomes).

• Multiplying Probabilities: Multiply probabilities when there are multiple different criteria/steps that each need to be fulfilled in a sequence (or multi-step process). Each step in the process has to be a success, and the probability has to account for the possibility that any given step might have been unsuccessful. This requires multiplication of probabilities rather than addition.

For example, using the skittles setup from above: if a question asks about the probability of drawing two consecutive red skittles, then that will require calculating the probabilities of each individual draw, and then multiplying them together. Another way to imagine multiplying probabilities is as a tree of possible outcomes.

If the odds of drawing a red skittle are ⅔, then on the first draw, there needs to be two branches: the branch where the first draw is successful (which will happen 2 out of 3 times) and the branch where the first draw is unsuccessful (which will happen 1 out of 3 times). Those are the odds of the first draw.

One must then repeat the process for my second draw. Since one may have been successful or unsuccessful on the first draw, the probability has to account for both possibilities when the final probability is calculated. The odds of ending up on one of the final four outcomes branches (for example red, red) = the odds of going down the first branch x the odds of going down the second branch.

It is sometimes possible to get a mixture of multiplied and added probabilities. This occurs in a multi-step process that has multiple possible successful outcomes. 

For instance, if a question asked what the possibility of drawing two skittles of the same color (red + red or blue + blue) would be. In that case, the tree still looks the same. But instead of focusing on the odds of one outcome branch, one must instead add up the odds of the two outcome branches that fulfill the goal.

This concept would be written out as this equation: (1/9+ 4/9= 5/9)
It’s worth noting that in the tree above, the probabilities are treated as independent. That is, the odds of one draw do not affect the odds of another draw. However, this is not always going to be the case. It will depend on whether or not I have outcomes that are mutually exclusive.

To understand how mutual exclusivity comes into play, and to look at our above concepts in action, here is question #46 from the December 2020 ACT:

The question wants to know the odds that two car owners drawn from our overall sample will be from the same age bracket. It can be any age bracket, so the question can be restated as: “what are the odds that the first car owner AND the second car owner picked will both be from the 16-25 age bracket OR the 26-45 age bracket OR the 46-60 age bracket?”

The question is asking to find two different car owners. This means that after selecting the first driver, they are no longer going to be in the pool of possibilities that will be selected from: they were selected in the first step, so they cannot be picked in the second step. Therefore, both the numerator and denominator of the probability fraction by 1 (to account for removing one successful possibility from our pool or possibilities). There is one fewer possible successful option and one fewer possible option overall.

So, for this problem, it is necessary to determine what the probability is that one will pick two car owners from each age bracket.

There are 80 16-25 year olds in the sample out of a possible 335 drivers. That means the odds of drawing a 16-25 year old are 80/335. The 2nd draw requires a different person from the same age bracket. So, there are 79 remaining drivers that could be successfully drawn from the 16-25 age bracket. There are also 334 total drivers now remaining. That means the odds of drawing the 2nd person from that age bracket are 79/334.

Both of those steps need to happen to fulfill the question’s criteria. Since step 1 AND step 2 need to be a success, the total probability of drawing two drivers from the 16-25 year old age bracket is (80/335)(79/334).

The process is then repeated for the other two age groups, since each separate age group can fulfill the specified criteria.

There are 155 people in the 26-45 age bracket. The odds of drawing someone on the first go are 155/335 and then 154/335 on the 2nd, since one still cannot draw the same person twice. That makes the odds of succeeding on both the 1st AND 2nd draw (155/335)(154/334).

Similarly, there are 100 people in the 46-60 age bracket. The first and second steps odd are 100/335 and 99/334, and the total probability is their product: (100/335)(99/334).

The odds of picking two drivers from each of the three different age brackets has been calculated. Each of those possibilities represents a successful outcome, and so the answer is the sum of their probabilities:

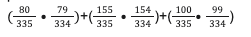
That means that A is the correct answer!

Key Takeaways

• Multiple solutions = addition
• Multiple steps = multiplication
• Mutual Exclusivity = Reduce the numerator and denominator