SubTopics
Coordinate Geometry-1
3.1 Coordinates
3.2 Drawing linear graphs (click to learn)*
3.3 Gradient of linear graphs (click to learn)*
3.4 Length and midpoint (extended)
Co-ordinate Geometry-2
3.5 Equations of linear graphs (click to learn)*
3.6 Parallel lines (click to learn)*
3.7 Perpendicular lines (extended) (click to learn)*
3.1 Coordinates
3.1. 2-D coordinates
What is the Cartesian plane?
- The Cartesian plane is a two-dimensional grid that has
- a horizontal scale, called the x-axis
- a vertical scale, called the y-axis
- The two axes meet at the origin
- where x and y are both 0
What are coordinates?
- Coordinates are a pair of numbers, x and y , that describe the location of a point on the grid
- They are written in brackets as (x , y )
- The point is
- x units on the horizontal scale
- y units on the vertical scale
- The origin is (0, 0)
- Positive values of x are to the right of the origin
- Negative values are to the left
- Positive values of y are above the origin
- Negative values are below
- Positive values of x are to the right of the origin
- For example, from the origin:
- (2, 5) is the point 2 units to the right and 5 units up
- (-1, -4) is the point 1 unit to the left and 4 units down
- “Along the corridor, up the stairs” helps to remember horizontal then vertical,(x , y)
Remember
- Check the scale on the coordinate grid!
- 1 square might not be 1 unit
Examples
(a) Write down the coordinates of the point A shown on the axes below.
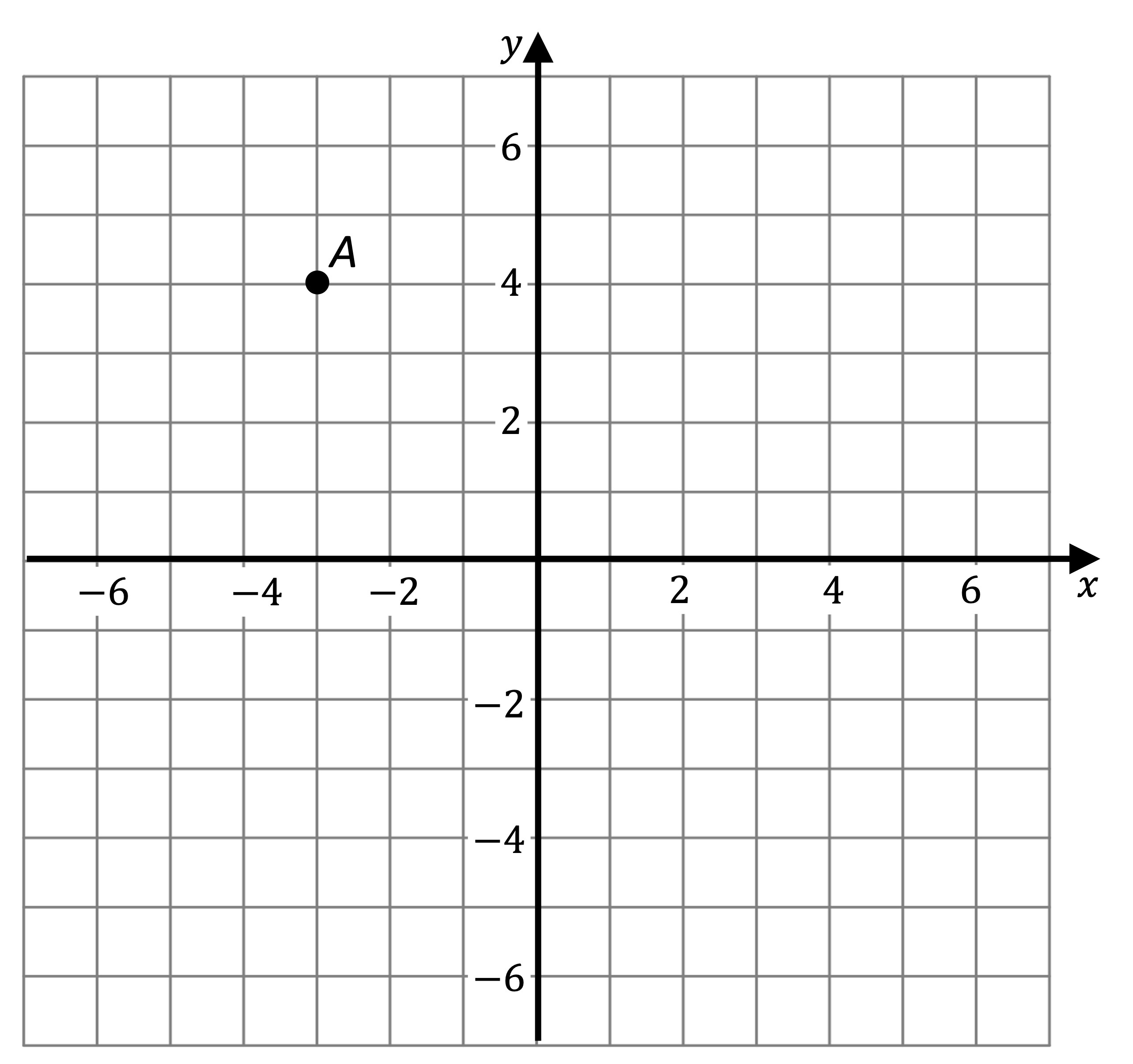
A is 3 units to left, so x is −3
A is 4 units up, so y is 4
Give your answer in brackets
(−3, 4)
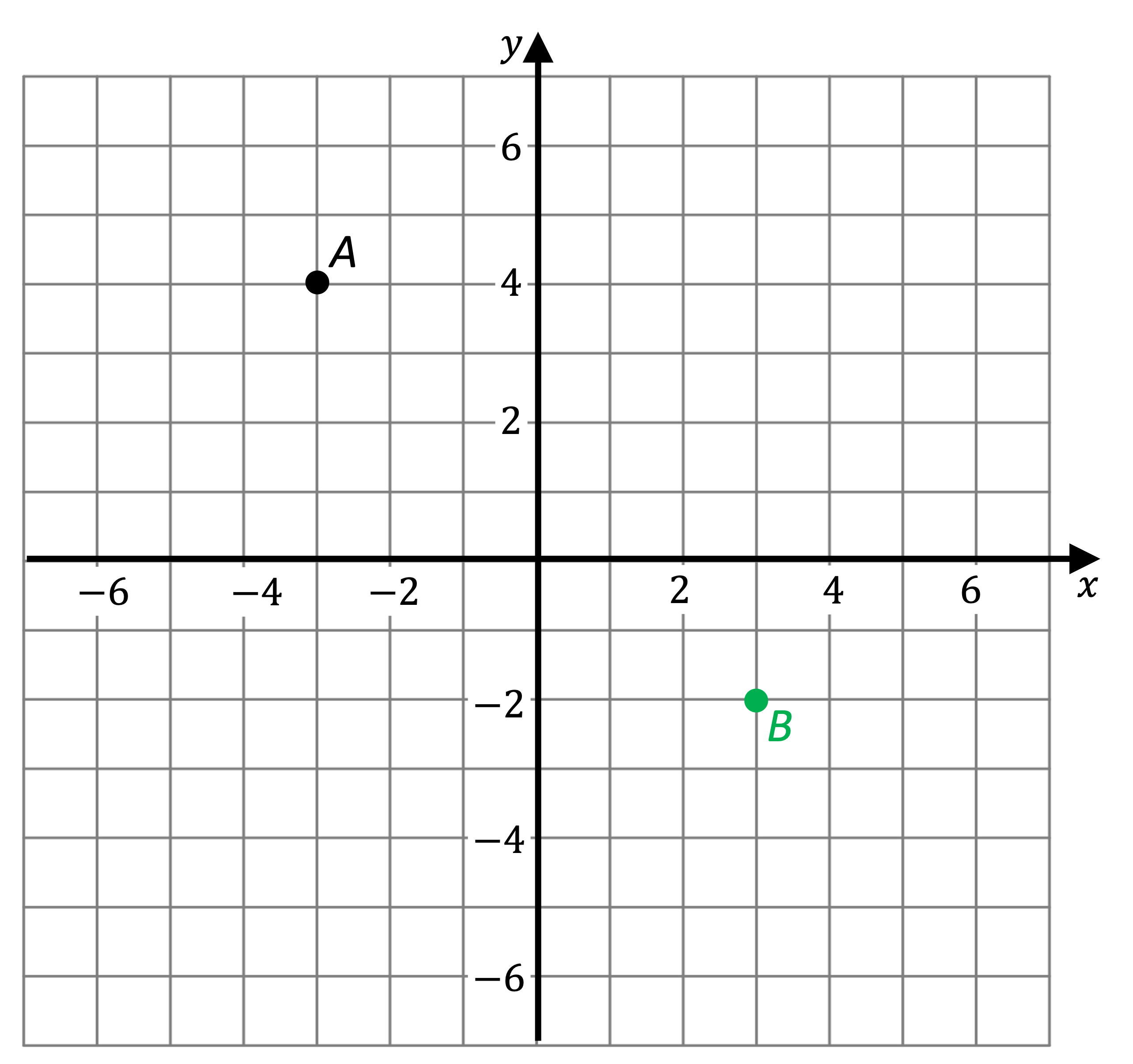
(b) Mark the point B with coordinates (3,- 2) on the same set of axes.
Start at the origin
Count 3 units right and two units down
Mark the point with a solid circle or cross and label it B
Midpoint of a line
Midpoint of a line
How do I find the midpoint of a line?
- The midpoint of a line will be the same distance from both endpoints
- You can think of a midpoint as being the average (mean) of two coordinates
- The midpoint of
is
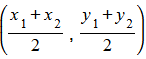
Worked Example
The coordinates of A are (−4, 3) and the coordinates of B are (8, −12).
Find the coordinates of the midpoint of AB.
The midpoint can be found using ((x1 + x2)/2, (y1 + y2)/2))
Substitute in the values of x and y from each point into their correct positions
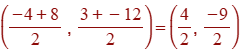
Simplify
(2, −4.5)
Gradient of a line
What is the gradient of a line?
- The gradient is a measure of how steep a straight line is
- A gradient of 3 means:
- For every 1 unit to the right, go up by 3
- A gradient of -4 means:
- For every 1 unit to the right, go down by 4
- A gradient of 3 is steeper than 2
- A gradient of -5 is steeper than -4
- A positive gradient means the line goes upwards (uphill)
- Bottom left to top right
- A negative gradient means the line goes downwards (downhill)
- Top left to bottom right
How to find the gradient of a line?
- Find two points on the line and draw a right-angled triangle
- Then gradient = change in y/change in x
- Or, in short, rise/run
- The rise is the vertical length of the triangle
- The run is the horizontal length of the triangle
- Put the correct sign on your answer
- Positive for uphill lines
- Negative for downhill lines
- Or, in short, rise/run
How to draw a line with a given gradient
> To draw a gradient 2/3 => the rise is 2 and the run is 3
It is positive (uphill): Move 3 units to the right and 2 units up
> To draw a gradient -5, convert it into a fraction: -5/1
=> The rise is 5 and the run is 1
It is negative (downhill) => Move 1 unit to the right and 5 units down.
Remember
- A lot of students forget to make their gradients negative for downhill lines!
Examples
(a) Find the gradient of the line shown in the diagram below.

Find two points that the line passes through: (0, 2) and (1, 5)
Use the grid to draw a right-angled triangle
Find the ‘rise’ (vertical length) and ‘run’ (horizontal length)

Work out rise/run = 3/1
Look to see if the line is uphill or downhill
uphill, so the gradient is positive
The gradient is 3
(b) On the grid below, draw the line with a gradient of -2 that passes through (0,1).
Mark on the point (0, 1)
-2 is the fraction -2/1
The rise is 2 and the run is 1. the line goes downhill (so 1 across, 2 down)

(c) On the grid below, draw the line with a gradient of 2/3 that passes through (0,-1).
Mark on the point (0,-1)
The rise is 2, the run is 3, the line goes uphill (so 3 across, 2 up)

Length of a line
How to calculate the length of a line?
The distance between two points with coordinates (x1, y1) and (x2, y2) can be found using the formula:
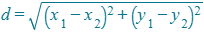
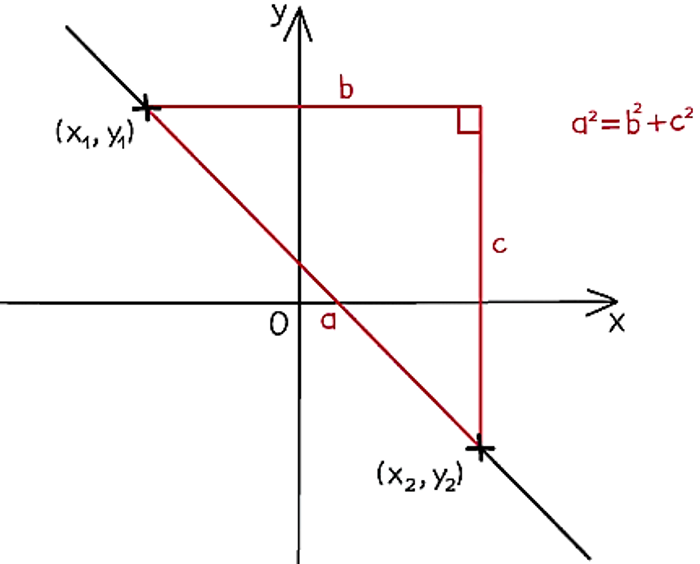
This formula uses Pythagoras’s theorem a2 + b2 = c2
It is applied to the difference in the x-coordinates and the difference in the y-coordinates
Remember
- Be extra careful when negative coordinates are involved
- It can help to put negative numbers in brackets to make your working clearer
- Example: -6 – (-8) = 2
Example
Point A has coordinates (3, -4) and point B has coordinates (-5, 2).
Calculate the distance of the line segment AB.
Using the formula for the distance between two points, d = ![]()
Substitute in the two given coordinates
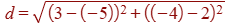
Be careful with the negative numbers: 3 – (-5) = 8 and (-4) – 2 = -6
Simplify

10 units
Leave a Reply