28. Absolute Value

Absolute value refers to the distance from zero of a value.

As such, it is always a positive value or zero

The absolute value of 7 is 7 because its distance from zero is 7; the absolute value of -9 is 9 because its distance from zero is 9.

The absolute value of an expression is indicated by enclosing the expression in a pair of vertical bars.

So, ∣5∣ indicates the absolute value of 5, which is 5; ∣-5∣ indicates the absolute value of -5, which is also 5.

This last example demonstrates a very important characteristic of the absolute value operation: because absolute value represents distance from zero, there are always two values that have the same absolute value: a positive number and the negative of that number (which happens to be called the additive inverse).

The only exception to this is that zero itself is neither negative nor positive, so only tlιe absolute value of zero yields zero.

The fact that there can be two values of an expression that yield the same absolute value means that when solving an equation for a variable, you need to take into account both of these values. Using the previous example, if we’re told that ∣x∣ = 5, we must realize that this means that x could be 5 or -5:

∣x∣ = 5 => x = 5 or x =-5

This splitting of the given equation into two equations is the primary mechanism for solving problems that involve an absolute value.

To illustrate this, let’s look at a more realistic example of a test problem.

Example:

∣3x – 2∣ = 7

If a and b are the solutions to the equation above, what is the value of ∣a — b∣ ?

Solution

Make two equations from the original, one where the expression 3x – 2 is set equal to 7. and one where it is set equal to -7: 3x – 2 = 7 or 3x – 2 = -7

Since one solution value of x is a and the other solution value of x is b. plug a in for x in the first equation and plug b in for x in the second equation. Note that it does not matter which value goes into which equation (it doesn’t matter if a or b is the greater value), because when we take the absolute value of the difference between them, the result would be the same regardless.

3a – 2 = 7

3b – 2 = -7

Subtract the second equation from the first in order to arrive at an equation containing the expression 3a — 3b, from which we can factor out a 3 and arrive at the desired expression a – b.

3a – 2 = 7

– (3b – 2 = -7)

3a – 3b = 14

Factor a 3 out of both terms on the left side of the equation in order to isolate the expression a — b. and then divide both sides of the equation by 3 in order to find the value of a – b.

3a – 3b= 14 => 3(a – b) = 14 => a – b = 14/3

The value of a — b is 14/3, so Ia — bl = 14/3. The answer is 14/3

Notes

For an alternate solution, split the original equation into the two valid equations and find each solution independently, assigning one to a and the other to b. Plug these values into the solve-for expression.

If you are skeptical about the respective values of a and b not being important to this problem, then you can try swapping them by plugging in -5/3 for a and 3 for b. and you will see (if you do it correctly) that in the end we will have I-14/3| which also evaluates to 14/3

Be aware, however, that some problems may have added conditions such as a > b. In these cases, you do have to assign values to the variables that agree with any conditions like a > b that are given to you in the problem statement.

Practice: 1

Directions: Find the solution(s) to each absolute value equation.

1. ∣x + 2∣ = 5 Ans. x = -7, x = 3

2. ∣-4x + 1∣ = 7 Ans. x = –³_/2, x = 2

3. ∣2x – 5∣ = 17 Ans. x = -6, x = 11

4. ∣3x – 3∣ = 0 Ans. x = 1

Absolute value inequalities again work in a similar way to absolute value equations, except that when we produce the second resulting inequality, we have to remember to flip the inequality sign (as if we multiplied by -1). If you think about the meaning of absolute value, which is that it represents distance from zero, this makes perfect sense: a negative number’s absolute value increases when the number becomes more negative, smaller, or farther from zero on the left side of the number line, while a positive number’s absolute value increases when the number becomes more positive, larger, or farther from zero on the right side of the number line.

For example. the inequality ∣x – 4∣ > 2 tells us that x – 4 is either greater than 2 or less than -2, because any values greater than 2 or less than —2 have an absolute value that is greater than 2.

|x – 4| > 2 => ∣x – 4∣ > 2 and x – 4 < -2

Absolute value inequalities that contain the greater-than sign result in two discontiguous simple inequalities; that is. there will be one inequality that’s unbounded on the lower end and bounded by a negative value on the upper end, and there will be a second inequality that has a positive lower bound, and it will be unbounded on the upper end. In-between the two ranges will be the values that are excluded.

For example, ∣x – 4∣ > 2 is equivalent to the two inequalities shown just above, and together they cover the range — to —2 (exclusive) and 2 (exclusive) to co, thereby excluding the range —2 to 2.

By contrast, absolute value inequalities with Iess than signs also produce two inequalities, but they end up collapsing into a compound inequality because they define one contiguous range of values. For example, the inequality ∣x — 4∣ < 2 tells us that x — 4 must be less than 2 and also greater than —2.

|x – 4| < 2 => ∣x – 4∣ < 2 and x – 4 > -2

These two inequalities will collapse into one compound inequality because the value of x has a lower bound at -2 and an upper bound at 2, which produces the compound inequality —2 < x — 4 < 2.

Practice: 2

(A):
(a) If |x| = 7, what is the value of x?

Sol. x = 7 or -x = 7

x = 7 or x = -7

(b) If |x – 3| = 4, what is the value of x?

Sol. (x – 3) = 4 => x = 4 + 3 => x = 7 or

-(x – 3) = 4 => -x + 3 = 4 => -x = 1 => x = -1

(c) If |x + 4| < 8, what is the value of x?

Sol: x + 4 < 8 => x < 8 – 4 => x < 4 or

-(x + 4) < 8 => x + 4 > -8 => x > -8 – 4 => x > -12

(d) If |x + 5| > 6, what is the value of x?

Sol: x + 5 > 6 => x > 6 – 5 => x > 1 or

-(x + 5) > 6 => x + 5 < -6 => x < -6 – 5 => x < -11

(e) If -9 < x < 3, express the interval using absolute value.

Sol: Midpoint of -9 & 3 = (-9 + 3)/2 = -6/2 = -3

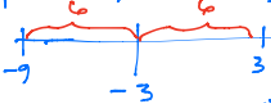
|x – c| < d where c = -3 and d = 6 => |x + 3| < 6

(B) Directions: Find all values of x that are solutions to each absolute value inequality.

1. ∣x + 2∣ < 5 Ans. 7 < x < 3

2. ∣-4x + 1∣ ≥ 7 Ans. x ≤ –³/₂ or x ≥ 2

3. ∣2x – 5∣ ≤ 17 Ans. -6 ≤ x ≤ 11

4. ∣3x – 3∣ > 0 Ans. x < 1 or x > 1 which means x ≠ 1

Practice Problems

1. ∣x – 4∣ = 8. What is one possible solution to the given equation?

Ans. -4 or 12

2. ∣8 – x∣ = 3. The value of one solution to the equation above is 5. What is the value of the other solution?

Ans. 11

3. 2∣1 – x∣ + 4∣1 – x∣ = 24. What is the positive solution to the given equation?

Ans. 5

RECAP

֍ Solve inequalities like you solve equations, but remember to flip the sign if you multiply or divide by a negative number.

֍ The pointy or small end of the inequality sign is the lesser side of the inequality; the open or big end of the inequality sign is the greater side of the inequality.

֍ Plugging in values is an easy way to check answers for inequality problems.

֍ In real world problems, correct answers often have to be integers, particularly if the problem involves items that cannot be divided into fractional amounts (books, shirts, etc.),

֍ Compound inequalities can be solved in one step as long as you are careful about flipping both inequality signs if you multiply or divide by negative numbers. Just make sure to apply the same operation to all three parts of the compound inequality.

֍ A point is in the solution set of a system of inequalities only if it satisfies both inequalities.

֍ When graphing linear inequalities in the xy-ρlane, use a solid line if there is a ≤ or ≥ sign in the inequality (because points on the line are solutions to the inequality), and use a dashed line if there is a < or > sign in the inequality (because points on the line are NOT solutions to the inequality).

Shade above the line to show the solution region when the y-variable is greater than the linear expression.

Shade below the line to show the solution region when the y-variable is less than the linear expression.

֍ Solutions to a system of linear inequalities must satisfy all the inequalities in the system.

If the inequalities are graphed on the same xy-plane, the solutions are located within the overlapping shaded regions and on any solid lines bounding those regions,

֍ You can solve absolute value equations by making two equations: one where the expression in the absolute value bars is set equal to the original value on the other side of the equation, and one where the expression is set equal to the negative of that value.

For example, ∣x∣ = 5 yields both x = 5 and x = -5.

Note that while the expression within the absolute value bars can have any value, positive or negative, the absolute value of the expression can never be negative, by definition.

For example, while ∣x∣ = 5 yields two possible solutions (x = 5 and x = —5), the equation ∣x∣ = —5 yields zero solutions because the absolute value of an expression can never be negative.

|x + a| > b => x + a > b and x + a < -b

|x + a| < b => x + a < b and x + a > -b => -b < x + a < b

Summary:

The absolute value of x, denoted |x|, is simply the distance of x from zero. For any real number A’,

1. If |x| = k and k > 0, then x = k or x = -k
2. If |x| < k and k > 0, then -k < x < k
3. If |x| > k and k > 0, then x < -k or x > k
4. |x| < 6 => x² < 36 => -6 < x < 6
5. |x| > 6 => x² > 36 => x < -6 or x > 6
6. |x – 5| = |5 – x|

Past Paper Questions:

|x + 3| = 6 and |y – 2| = 7 For the equations shown above, which of the following is a possible value of x – y?
A. -14	B. -4	C. -2	D. 14
B
To solve the first equation, set x +3 = 6 and set x + 3 = -6. If x + 3 = – 6. then the absolute value would still be 6. So. x can be either 3 or -9. To solve for y. Either y = 9 or y = -5. To find the correct answer, you need to try the different combinations. One combination is x = -9 and y =    5. So. x – y = -9 – (-5) = -4

How many solutions exist to the equation |x| = |2x – 1| ?
A. 0	B. 1	C. 2	D. 3
C
If |x| = |2x – 1|, either x = 2x – 1 or —x = 2x     1. The solutions to these equations are 1 and 1. respectively.

For what value of x is |2x + 3| + 5 = 0?
A. -4	B. 0	C. 4	D. There is no such value of x
D
Simply Plug In the Answers to get a solution. Option (A) is incorrect: |2(-4) + 3| + 5 = 0 could be rewritten as | – 8 + 3| + 5 = 0. or |- 5| + 5 = 0. As long as you remember that the absolute value of a number is always positive, it is clear that this gives you 5 + 5 = 0. Since this is clearly untrue Option (B) is incorrect: If x is 0 . then the original equation says |2(0) + 3| + 5 = 0 or 8 = 0. This is clearly not true Option (C) is incorrect. When you put 4 in for x, you get |2(4) + 3| + 5 = 0. or 16 = 0. This is clearly not true, so choose (D). Apparently. there is no such value of x !

Which of the following expressions is equal to -1 for some values of x?
A. |1 – x| + 6	B. |1 – x| + 4	C. |1 – x| + 2	D. |1 – x| – 2
D
By definition, the absolute value of any expression is a nonnegative number. Therefore. |1 — x| + 6 > 0, |1 — x| + 4 > 0, and |1 — x\ + 2 > 0. Only |1 — x| — 2 could be a negative number. |1 – x| – 2 = -1 =>|1 – x | = 1 =>x = 2or x = 0

If |2z + 7| = 5, which of the following could be the value of x?
A. -6	B. -4	C. -2	D. None
A
|2z + 7| =5 => 2x + 7 = 5 => 2x = -2 =>x = -1 or 2x + 7 = -5 => 2x = —12 => x = —6

For what value of x is |x – 1| – 1 equal to 1?
A. -1	B. 0	C. 1	D. None
A
|x – 1| – 1 = 1 => |x – 1| = 2 => x – 1 = 2 or x – 1 = -2 => x = 3     or x = —1

For what value of n is 3 – |3 – n| equal to 3?
A. 1	B. 2	C. 3	D. 4
C
3 – |3 – n| = 3 => -|3 – n| = 0 Subtract 3 from each side. If -|3 – n| = 0 or |3 – n| = 0. then 3 – n = 0, Thus n = 3.

Which of the following expressions is equal to 0 for some value of x?
A. 5 + |x + 5|	B. 5 + |x – 5|	C. -5 +|x + 5|	D. None
C
The expressions |x + 5| or |x — 5| can never be a negative number. Thus 5 + |x + 5| or 5 + |x — 5| cannot equal zero. The expression —| x – 5| can never be a positive number. Thus —5 – |x – 5| cannot equal zero. If -5 + |x + 5| = 0. then |x + 5| = 5, when x = 0

Solve for x: |x – 1| = 4
A. 4 or -3	B. 5 or 2	C. 5 or —3	D. 3 or -3
C
Consider the two possibilities: If the quantity inside the absolute value sign is nonnegative, then| x — 1| = x — 1 = 4, so x = 5 If the quantity inside the absolute value sign is negative, then |x – 1| = -(x – 1) = 4, so —x + 1 = 4 => -x = 3 => x = 3 The two possible solutions for x are 5 or −3. Verify that both roots satisfy the original absolute value equation

Solve for x: |2x + 3| + 4 = 5
A. 1 or -5	B. 1 or -4	C. -1 or -2	D. 2 or -2
C
If |2x + 3|+4 = 5, then |2x + 3| = l. Thus, If 2x + 3 = 1, so 2x = 1 – 3 = -2 and x = -2/2 = -1; If 2x + 3 = -1, so 2x = -1 – 3 = -4 and x = -4/2 = -2

Solve and check: |x – 3| = 2x
A. 1	B. -3	C. -1	D. 3
A
|x — 3| = 2x, so, Case 1: x — 3 = 2x and Case 2: x – 3 = -2x Solving Case 1: x – 3 = 2x =>-3 = 2x – x (Subtracting x from both sides) => -3 = x Solving Case 2: x – 3 = -2x => x + 2x – 3 = 0 (Adding 2x to both sides) => 3x – 3 = 0 => 3x = 3 (Add 3 to both sides) => x = 1 The two potential solutions are: x = —3 and x  = 1 Check: If x = —3, then |-3 – 3| = 2(-3) => |-6| ≠ -6 Check: If x = 1, then |x — 3| = 2x => |1 – 3| = 2(1) => |-2| = 2 Hence, x = 1 is the only root of the absolute value equation.

Solve the solution set of |2x – 1| ≤ 7.
A. -4 ≤ x ≤ 0	B. 5 ≤ x ≤ 4	C. -3 ≤ x ≤ 4	D. 4 ≤ x ≤ 4
C
If |2x – 1| ≤ 7, then -7 ≤ 2x – 1 ≤ 7. Add 1 to each member of the combined inequality: -7 ≤ 2x – 1 ≤ 7 + 1          +1 + 1 -6 ≤ 2x       ≤8 Divide each member of the combined inequality by 2: -6/2 ≤ 2x/2 ≤ 8/2 => -3 ≤ x ≤4 Graph the solution set: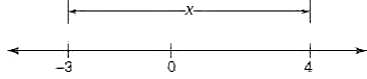

If 5 < |2 – x| < 6 and x > 0, what is one possible value of x?
A. 2	B. -5	C. 7.5	D. 3.5
C
If 2 – x ≥ 0. then 5 < 2 — x < 6. so, 3 < —x < 4. Multiplying each term of the inequality by -1 gives -3 > x > -4. Since it is given that x > 0, disregard this solution. – If 2 – x < 0, then 5 < —(2 — x) < 6 or. equivalently, 5, so, 5 + 2 < x < 6 + 2 and 7 < x < 8. Therefore, x can be any number between 7 and 8, such as 7.5.

|n – 1| < 4. How many integers n satisfy the inequality above?
A. Two	B. Five	C. Seven	D. Nine
C
If |n— 1| < 4. then -4 < n – 1 < 4, so -4 + 1 < n < 4 + 1 and -3 < n < 5. There are seven integers between —3 and 5: -2, —1, 0, 1, 2, 3, and 4

If |x| ≤ 2 and |y| ≤ 1, then what is the least possible value of x – y?
A. -3	B. -2	C. -1	D. 0
A
If |x| ≤ 2 and |y| ≤ 1, then -2 ≤ x ≤ 2 and -1 ≤ y ≤ 1. The least possible value of x – y is -2 – 1 = -3

If |½ x| ≥ ½ then which statement must be true?
A. x ≤ —2 or x ≥ 2	B. x ≤ —1 or x ≥ 1	C. x ≤ —½ or x ≥ 1/2	D. —1 ≤ x ≤ 1
B
|½ x| ≥ ½ then either ½ x ≥ ½ so x ≥ 1 or ½ x ≤ – ½ so x ≤ —1.

If ½ |x| and |y| = x + 1, then y2 could be
A. 2	B. 3	C. 4	D. 9
D
If ½ |x| = 1, then |x| = 2. so x = ±2. If x = —2. then |y| = x + 1 = -1. which is impossible. If x = 2, then |y| = x + 1 = 3, so y = ±3 and y2 = (±3)2 = 9

If (|a + 3|)/2 = 1 and 2|b + 1| = 6, then |a + b| could equal any of the following EXCEPT
A. 1	B. 3	C. 5	D. 7
D
If (|a + 3|)/2 = 1, then |a + 3| =2, so a + 3 = 2 or a + 3 = -2. Hence, a = —1 or a = -5. If 2|b+1| = 6. then |b + 1| = 3, so b + 1 = 3 or b + 1 =-3. Hence, b = 2 or b = —4. Then |a + b| could equal the following: – |-1 + 2| = 1 => – | — 1_+ (—4)| = 5  => -|-5 + 2| = 3 => – I — 5+(—4)| = 9 Thus, |a + b| could not equal 7

For what value of x is |1 + x| = |1 – x|?
A. -1	B. 0	C. 1	D. No value
B
To find the value of x that satisfied |1 + x| = |1 — x|, if any. plug the answer choices into the equation to see if one works. lf x = 0, |1 + 0| = |1 – 0| = 1.

|t – 7| = 4 and |9 – t| = 2 What value of t satisfies both of the above equations?
A. 3	B. 7	C. 9	D. 11
D
If |t – 7| = 4, then t – 7 = 4 or t — 7 = -4. Then t = 11 or t = 3 If |9 – t| = 2, then 9 – t = 2 or 9 – t = -2. Then t = 7 or t = 11

If |- 3y + 2| < 1, what is one possible value of y?
A. 0	B. ½	C. 9/2	D. 5
B
If | – 3y + 2| < 1. then -1 < -3y + 2 < 1, so, -1 – 2(-3y/-3) > -1/-3 =-> 1 > y > ⅓ Hence, y can take on any value between ⅓ and 1 such as ½.

If |x – 16| ≤ 4 and |y – 6| ≤ 2, what is the greatest possible value of x — y?
A. 2	B. 4	C. 16	D. 20
C
It is given that |x – 16 ≤ 4 and |y – 6| ≤ 2. The greatest possible value of x — y occurs when x takes on its greatest value and. at the same time, y takes on its smallest value. If |x — 16| ≤ 4, then — 4 ≤ x — 16 ≤ 4. Adding 16 to each member of the inequality makes 12| ≤ x ≤ 20. Hence, the greatest value of x is 20. -If |y — 6| ≤ 2. then —2 ≤ y — 6 ≤ 2. Adding 6 to each member of the inequality makes 4 ≤ y ≤ 8. Hence, the smallest value of y is 4 . – The greatest value of x – y is 20 – (4) = 16.

|3x – 15| = 18. What is the product of all possible values of x ?
A. -11	B. -10	C. -9	D. -8
A
Solve the absolute value equation for both cases. |3x — 15| = 18 => 3x — 15 = 18 => 3x = 33 => x = 11 or |3x — 15| = -18 => 3x — 15 = —18 => 3x = —3 => x = —1 Multiply the solutions. -1 x 11 = -11

|x — y| = d and x > y, which of the following cannot be the value of y — x ? l. d    ll. —d    lll. |y – x|
A. I	B. II	C. I and II	D. I and III
D
We know x > y so y — x is negative. |x — y|= d => y — x = —d That means (y — x) cannot equal these choices: I. d and III. |y – x|

a = ||x|3 — |x — y|2 — y + x |. If x = — 2 and y = 5, a =?
A. 47	B. 48	C. 49	D. 50
B
Substitute and solve for a. a = || – 2|3 – | – 2 – 5|2 – 5 + (-2)| = |23 – 72 – 5 – 2 = |8 — 49 — 5 — 2| = |-48|= 48

If |4x — 12| + 15 = 19, what are the possible values of x?
A. x = 4 and x = 2	B. x = 4 and x = 1	C. x = 3 and x = 2	D. x = 1 and x = 2
A
|4x – 12l + 15 = 19 => |4x – 12| = 19 – 15 = 4 => 4x – 12 = ±4 => x = 4 and x = 2

|x — y| = 5 Which values of x and y make the above equation NOT true?
A. x = — 8, y = —3	B. x = 12, y = 7	C. x = -20, y = -25	D. x = -5, y = 10
Answer choice a: |(-8) – (-3)| = |(-8) + 3| = | – 5| = 5 Answer choice b: |12 – 7| = |5| = 5 Answer choice c: |(-20) – (-25)| = |(-20) + 25 = |5| = 5 Answer choice d: |(-5) – 10| = | – 15| = 15 Therefore, the values of x and y in answer choice d make the equation NOT true.

|-1 – 2| – |5 – 6| – |-3 + 4| = ?
A. -5	B. -3	C.	D. 5
C
First, determine each of the three absolute values: |-1 – 2| = |-3| = 3; |5 – 6| = |-1| = 1 and |-3 + 4| = |1| = 1 Then combine the three results: 3 — 1 — 1 = 1.

|-2 – 3| – |2 – 3| = ?
A. -2	B. -1	C. 0	D. 4
D
| — 2 — 3| = | — 5| = 5, and |2 — 3| = | — 1| = 1. Performing subtraction: 5 — 1 = 4 The concept of absolute value can be incorporated into many different types of problems on the new SAT. including those involving algebraic expressions, equations, and inequalities, as well as problems involving functional notation and the graphs of functions.

|7 – 2| – |2 – 7| = ?
A. -14	B. -9	C. -5	D. 0
D
|7 – 2| – |2 – 7| = 5 – | – – 5| = 5 – 5 = 0

For all integers a and b, where b ≠ 0, subtracting b from a must result in a positive integer if:
A. |a — b| is a positive integer	B. (a/b) is a positive integer	C. (b — a) is a negative integer	D. (a + b) is a positive integer
C
If b — a is a negative integer, then a > b. in which case a – b must be a positive integer. (When you subtract one integer from another, the result is always an integer.) Choice (A), which incorporates the concept of absolute value, cannot be the correct answer, since the absolute value of any integer is by definition a positive integer.

|-4| – |-8| + |-2||-3| = ?
A. -2	B. 2	C. 4	D. 6
B
|-4| – |-8| + |-2||-3| = 4 – 8 + (2)(3) = -4 + 6 = 2

Which of the following points is NOT in the solution set of | — x|— | — y| = 1?
A. (-2, -3)	B. (-7, -6)	C. (4, -3)	D. (-5,4)
A
Plug each point {x, y) from the answer choices into the question. All of them make the equation true except (A)

If |x| ≠ 0, which of the following statements must be true?
A. x is positive	B. 1/x is positive	C. x2 is positive	D. x3 is positive
C
The statement says that x is not zero which means is can be either positive or negative. Any number, positive or negative, squared will always be positive. This eliminates (A) and )B). If x were negative, then x3 would also be negative eliminating (D).

If y = |x| + 1, what is y when x = — 5?
A. -6	B. -4	C. 4	D. 6
D
∣x∣ means the absolute value of x, which is how far x is from 0 on the number line. −5 is 5 units away from 0 , so ∣−5∣ = 5, and 5 + 1 = 6.

If x = 7, then |5 — x| = ?
A. -2	B. 2	C. 7	D. 12
B
Plug in 7 for x, and you get ∣5 – 7| = ∣−2∣ = 2. (A) is a partial answer. Remember, the absolute value of a number must be positive

Find the value of each expression: |— 6 — 7|
A. -13	B. 13	C. 1	D. -1
A
∣−6 – 7∣ = ∣−13∣ = 13

Find the value of each expression. −∣−9∣
A. 3	B. -3	C. 9	D. -9
D
−∣−9∣ = −(9) = −9

Find the value of each expression. −∣−12+(−4)∣
A. -8	B. -16	C. 8	D. -16
B
-|12 + (-4)| = -|-12 – 16| = -|-16| = -16

Calculate the value of ∣−5∣ − ∣12∣ + ∣−4∣. − 3∣
A. 10	B. -24	C. 5	D. -5
C
∣−5∣ − ∣12∣ + ∣−4∣.− 3∣ = 5 – 12 + (4)(3) = 5 – 12 + 12 = 5

Solve the equation |y| + 4 = 9
A. 4, -4	B. 9, -9	C. 5, -5	D. 13, -13
C
Begin by subtracting 4 from both sides in order to get the absolute value by itself on one side. The result is the equation |y| = 5, so y = 5 or -5.

Solve the equation ∣2x + 3∣ = 11
A. 4, -7	B. -4, 7	C. -8. 14	D. 1.5, -5.5
A
|2x + 3| = 11 => 2x + 3 = 11 or 2x + 3 = -11. 2x + 3 = 11 => 2x = 8 => x = 4 or 2x + 3 = -11 => 2x = -14 => x = -7 Therefore, the two solutions are x = 4 and x = -7.

Solve for y: 3∣2y∣ + 2 = 17
A. 17/3, -17/3	B. 15/3, -15/3	C. 17/12, -17/12	D. 5/2, -5/2
D
Begin by isolating the absolute value. 3|2y| + 2 = 17 Subtract 2 from both sides: 3|2y| = 15 Divide both sides by 3: |2y| = 5 Therefore: 2y = 5 or 2y = —5 => y = 5/2 or y = -5/2

If f(x) = 2∣x∣3, what is the value of f(−3)?
A. 18	B. 24	C. 54	D. 108
C
f(x) = 2|-3|3 = 2(3)3 = 2(27) = 54

Solve for p: ∣p – 2∣ = 12
A. p = 10, −14	B. p = 14, −14	C. p = 10, −10	D. p =14, −10
D
|p – 2| = 12 => p – 2 = 12 or p – 2 = -12 => p = 14 or p = -10

Solve for q: 4 = ∣1 – 3q∣
A. q = −1, 5/3	B. q = 1, −5/3	C. q = 1, 5/3	D. q = −1, −5/3
A
4 = |1 — 3q| = 4 = 1 – 3q => 4 – 1 – 3q => 3 = -3q => q = -1 or 4= -(1 – 3q) => 4 = -1 + 3q => 5 = 3q => q = 5/3

Solve for r: ∣5 – 3(2 – r)∣ = 0
A. r = −⅓	B. r = ⅓	C. r = ⅓, -⅓	D. r = −3, -3
B
|5 —3(2 —r)| = 0 Simplify the expression inside the absolute value signs: |5 – 6 + 3r| =0 |-1 + 3r| = 0 The only way this equation can be true if —1 + 3r = 0, or 3r = 1, so r = ⅓

What is the value of −∣−4 + (−7)∣ + ∣(−13)(5)∣?
A. 54	B. 62	C. 68	D. 76
A
-|-4 + (-7) | + | (-13) (5)| = – |11| + |-65| = -(11) + 65 = 54

What is the sum of the solutions of the equation ∣2x − 7∣ = 11?
A. −9	B. −7	C. 5	D. 7
D
The equation |2x — 7| = 11 is true when 2x — 7 = 11 and when 2x — 7 = —11. 2x – 7 = 11 => 2x = 18 => x = 9 or 2x – 7 = -11 => 2x – -4 => x = -2 Therefore, the two solutions are 9 and -2. and their sum is 7.

If 3 < ∣x∣ < 5 and 4 < ∣y∣ < 6, which of the following must be true?
A. y < x	B. x < y	C. xy > 0	D. ∣xy∣ > 12 E. ∣x + y∣ > 7
D
The best way to approach this problem is to plug in numbers for x and y.  For instance, try x = 4.5, and y = 4.5. (A) and (B) cannot be true. Now make x = —4.5. (C) and (E) cannot be true.

What is the positive difference between the two solutions of 3 = ∣1 – 2q∣?
A. 1	B. 2	C. 3	D. 4
C
The equation 3 = |1 – 2q| is true when 1 – 2q = 3 and when 1 1 – 2q = 3 => -2q = 2 => q = -1 or 1 – 2q = -3 => -2q = -4 => q = 2 Finally, 2 – (-1) = 2 + 1 = 3.

If f(x) = 3∣x∣3, what is the value of f(−2)?
A. 8	B. 12	C. 18	D. 24
D
Compute: f(-2) = 3| – 2|3 = 3(2)3 = 3(8) = 24

∣2y – 4∣ = 6, y =?
A. −5,1	B. −8	C. −4,3	D. 5, -1
D
|2y – 4 = 6| means that 2y – 4 = 6 or 2y – 4 = -6 Solving the first equation, y = 10/2 = 5, and solving the second equation gives y a value of -1. Therefore, y = both 5 and —1.

For what value of n is ∣n − 1∣ + 1 equal to 0?
A. 0	B. 1	C. 2	D. There is no such value of n
D
If the value of |n — 1| + 1 is equal to 0, Subtracting 1 from both sides of this equation gives |n – 1|  = —1. The expression |n — 1| on the left side of the equation is the absolute value of n — 1, and the absolute value can never be a negative number. Thus |n — 1| = —1 has no solution. Therefore, there are no values for n for which the value of |n — 1| + 1 is equal to 0. Choice A is incorrect because |0 — 1| + 1 = 1 + 1 = 2. not 0. Choice B is incorrect because |1 — 1| + 1 = 0 + 1 = 1, not 0. Choice C is incorrect because |2 — 1| + 1 = 1 + 1 = 2, not 0

|2x – 3| ≤ 7 and |x – 2| ≤ 4. If x is an integer, what value of x is a solution for one inequality but not the other?
A. 6	B. 5	C. 4	D. 3
A
Solve the absolute value inequality. |2x – 3| ≤ 7 2x – 3 ≤ 7 => 2x ≤ 10 => x ≤ 5. 2x – 3 ≥ -7 => 2x ≥ -4 => x ≥ -2. |x – 2| ≤ 4 x – 2 ≤ 4 => x ≤ 6 x – 2 ≥ -4 =>-x ≥ -2. The integer x = 5 satisfies the first inequality but appears to not satisfy the second inequality but it is not outside the second’s solution set. Notice that 6 is a solution to the second inequality but not to the first inequality. OR Express the first inequality as a compound inequality to analyze the absolute value constraint: -7 ≤ 2x – 3 ≤ 7 Step 1: Solve the first inequality The first inequality |2x — 31 ≤ 7 is solved as: Express the first inequality as a compound inequality to analyze the absolute value constraint: -7 ≤ 2x – 3 ≤ 7 Adding 3 to all parts gives: -4 ≤ 2x ≤ 10 Dividing by 2 gives: -2 ≤ x ≤ 5 The integers satisfying this are {-2, -1, 0, 1, 2, 3, 4, 5}. Step 2: Solve the second inequality The second inequality |x – 2| ≤ 4 is solved as: Express the second inequality as a compound inequality: -4 ≤ x – 2 ≤ 4 Adding 2 to all parts gives: —2 ≤ x ≤ 6 The integers satisfying this are {-2, -1, 0, 1, 2, 3, 4, 5, 6}. Step 3: Identify the exclusive solution The set of integers for the first inequality is S1 and for the second is S2. The values that are in S2 but not S1 are the elements greater than 5, which is only 6. There are no integers in S1 that are not in S2

Which of the following inequalities create the graph: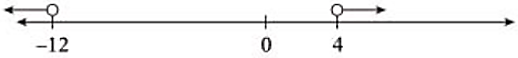
A. ∣x − 8∣ < 4	B. |x — 4| < 8	C. |—x —4| > 8	D. |x – 8|> 4
C
The arrows are pointing out. Choose a greater than inequality. The midpoint of —12 and 4 is -4. This is only true for Choice D. Check your solution. | — x – 4| > 8 —x — 4 < 8 => —x > 12 => x < -12. —x — 4 => —x < —4 => x > 4

Which of the following gives the solution set for the equation ∣(x + 3)/2∣ = 5?
A. [7∣	B. {−13}	C. (−13, 7]	D. [−7, 13]
C
Step 1: Setting up the two possible equations The absolute value equation |(x + 3)/2| = 5 is equivalent to two separate linear equations: •   (x + 3)/2 = 5 •   (x + 3)/2 = -5 Step 2: Solving the first equation (x + 3)/2 = 5 => x + 3= 10 (Multiplying both sides by 2) => x = 7 (Subtracting 3 from both sides) Step 3: Solve the second equation (x + 3)/2 = -5 => x + 3 = -10 (Multiplying both sides by 2) => x = -13 (Subtracting 3 from both sides) Step 4: Form the solution set The solutions are x = 7 and x = —13. The solution set is { —13,7}.

Word Problems:

In a certain greenhouse for plants, the Fahrenheit temperature, F, is controlled so that it does not vary from 79° by more than 7°. Which of the following best expresses the possible range in Fahrenheit temperatures of the greenhouse?
A. |F – 79| ≤ 7	B. |F — 79| > 7	C. |F – 7| ≤ 79	D. |F – 7| > 79
A
Since the temperature. F, can range from 7° below 79° to 7° above 79°, the positive difference between F and 79° is always less than or equal to 7° , which is expressed by the inequality |F – 79| ≤ 7.

An ocean depth finder shows the number of feet in the depth of water at a certain place. The difference between d, the actual depth of the water, and the depth finder reading, x, is |d – x| and must be less than or equal to 0.05d. If the depth finder reading is 620 feet, what is the maximum value of the actual depth of the water, to the nearest foot?
A. 620	B. 625	C. 652	D. 653
C
It is given that |d — x| ≤ 0.05d and x = 620. Hence, |d – 620| ≤ 0.05d => -0.05d ≤ d – 620 ≤ 0.05d => 620 – 0.05d ≤ d ≤ 620 + 0.05d The maximum depth, d, must satisfy the inequality d < 620 + 0.05d so, 0.95d ≤ 620 and d ≤ 620/0.95. Since d ≤ 652.63, to the nearest foot, the maximum depth is 652.

The weights of 5 boxes of screws vary from 2.85 pounds to 3.45 pounds. If w represents the weight, in pounds, of one of these boxes, which of the following must be true?
A. |w – 2.85| ≤ 0.3	B. |w – 3.15| ≤ 0.3	C. |w – 5| ≤ 0.3	D. |w – 0.3| ≤ 3.15
B
The weight that is midway between the smallest and greatest box weights is (2.85 + 3.45)/2 = 6.3/2 = 3.15 pounds. The difference between the smallest or greatest box weights and 3.15 pounds is 0.3 pounds since 3.45 – 3.15 = 0.3. If w represents the weight of any one of the 5 boxes, then the positive difference between w and 3.15 pounds must be less than or equal to 0.3 pounds, which can be expressed using the absolute value inequality |w – 3.15| ≤ 0.3.

An art class of 20 students took a final exam and ten of the students scored between 78 and 86 on the exam. If s is defined as the scores of the ten students, which of the following describes all possible values of s?
A. ∣s – 82∣ = 4	B. ∣s + 82∣ = 4	C. ∣s – 82∣ < 4	D. ∣s + 82∣ < 4
C
78 < Marks < 86 midpoint = (78 + 86)/2 = 164/2 = 82 and distance of midpoint from endpoint = 86 – 82 = 4 the interval expressed with absolute value is, |x – midpoint| < distance => |s – 82| < 4

At a bottling company, a computerized machine accepts a bottle only if the number of fluid ounces is greater than or equal to 53/7, and less than or equal to 64/7. If the machine accepts a bottle containing f fluid ounces, which of the following describes all possible values of f?
A. ∣f – 6∣ < 4/7	B. ∣f – 6∣ ≤ 3/7	C. ∣f + 6∣ > 4/7	D. ∣6 – f ∣ ≤ 4/7
A
Given that 53/7 < f < 64/7. Midpoint = ½ (53/7 +64/7) = 6 and distance of midpoint from endpoints = 4/7 the interval can be expressed with absolute value by using, |x – midpoint|≤  distance => |f – 6| ≤ 4/7

At the Moo-Moo Milk Company, machine X fills a canon with milk, and machine Y eliminates the milk carton if the weight is less than 450 grams or greater than 500 grams. If the weight of the carton that will be eliminated by machine Y is E, in grams, which of the following describes all possible values of E?
A.|E – 475| < 25	B. |E + 475| < 25	C. |E – 500| > 450	D. |475 – E| = 25
D
Step 1: Identifying the condition for elimination: The problem states that a carton is eliminated if its weight E is less than 450 grams or greater than 500 grams. This can be expressed as the inequalities E < 450 or E > 500. <? Step 2: Converting to a single absolute value inequality The midpoint of the acceptable weight range (450 to 500), which is (450 + 500)/2 = 475 grams. The distance from the midpoint to the boundaries is 500 – 475 = 25 grams. The eliminated weights are those outside this range, meaning their distance from the midpoint is greater than 25 grams. => | E — 475| > 25 => |475 – E| > 25

At a bottling company, machine A fills a bottle with spring water and machine B accepts the bottle only if the number of fluid ounces is between 79/10 and 81/10. If machine B accepts a bottle containing x fluid ounces, which of the following describes all possible values of x?
(A) |x – 8| = 1/10	(B) |x + 8| = 1/10	(C) |x – 8| < 1/10	(D) |x + 8| < 1/10
C
Step 1: Identifying the given range for x: 7 9/10 to 81/10. Step 2: Converting the fractions to decimals: 7 9/10 = 7.9 and 81/10 = 8.1 Step 3: Expressing the range as an inequality: 7.9 < x < 8.1 Step 4: Rewriting the inequality using the absolute value function: |x – 8| < 0.1 => |x – 8  < 1/10

At the O.K Daily Milk Company, machine X fills a box with milk, and machine Y eliminates milk-box if the weight is less than 450 grams, or greater than 500 grams. If the weight of the box that will be eliminated by machine Y is E, in grams, which of the following describes all possible values of E?
A. ∣E – 475∣ < 25	B. ∣E – 500∣ > 450	C. ∣475 – E∣ = 25	D. ∣E – 475∣ > 25
D
Machine Y accept milk if its weight, 450 < E < 500 => midpoint of interval = (450 + 500)/2 = 475 and distance of midpoint from end point = 475 – 450 = 25 then, the interval can be expressed with absolute value by using, | x – midpoint | < distance => |E – 475| ≤ 25 then the interval in which machine eliminate the milk, will be E – 475 > 25 OR In the given scenario, machine Y eliminates a box if its weight is less than 450 grams or greater than 500 grams. Therefore, the weight of the box eliminated by machine Y, denoted as E, will have a value that is not within the range of 450 to 500 grams. This can be represented as E < 450 or E > 500. To express this in mathematical notation, we can rewrite the inequalities as: E – 450 < 0 (equation 1) => E < 450 E – 500 > 0 (equation 2) => E > 500 Combining these two inequalities, we can rewrite it as: E – 475 > 25 (since 475 is the midpoint between 450 and 500) This can be further simplified as: |E – 475| >25 Analysis of the answer choices: A)  |E — 475| < 25 – This means that the weight of the box is within 25 grams of 475. But we know that the weight of the box is either less than 450 grams or greater than 500 grams. This option does not describe all possible values of E. B)  |E — 500| > 450 – This means that the weight of the box is more than 450 grams away from 500. But we know that the weight of the box is either less than 450 grams or greater than 500 grams. This option does not describe all possible values of E. C)  |475 — E| = 25 – This means that the weight of the box is either 450 grams or 500 grams. This option does not describe all possible values of E. D)  |E — 475| > 25 – This means that the weight of the box is more than 25 grams away from 475. Since the weight of the box is either less than 450 grams or greater than 500 grams, this option describes all possible values of E.